How To Find Binomial Probability On Statcrunch
Objectives
By the stop of this lesson, you will be able to...
- explain the logic of hypothesis testing
- test hypotheses about a population proportion
- test hypotheses well-nigh a population proportion using the binomial probability distribution
For a quick overview of this department, watch this short video summary:
The Logic of Hypothesis Testing
One time we accept our aught and alternative hypotheses chosen, and our sample information collected, how exercise nosotros choose whether or not to refuse the null hypothesis? In a nutshell, information technology's this:
If the observed results are unlikely assuming that the naught hypothesis is true, we say the result is statistically significant, and we reject the null hypothesis. In other words, the observed results are and so unusual, that our original assumption in the null hypothesis must not have been right.
Your textbook references three different methods for testing hypotheses:
- the classical approach
- P-values
- confidence intervals
Because P-values are so much more widely used, we will be focusing on this method. Yous volition exist required to include P-values for your homework and exams.
If y'all're interested in learning any of these other methods, experience free to read through the textbook.
P-Values
In general, we define the P-value this manner:
The P-value is the probability of observing a sample statistic equally farthermost or more farthermost than the i observed in the sample bold that the aught hypothesis is true.
The Sample Proportion
In Section 8.2, we learned about the distribution of the sample proportion, so permit'due south do a quick review of that now.
In general, if nosotros permit x = the number with the specific characteristic, then the sample proportion, 
, (read "p-hat") is given by:
Where is an estimate for the population proportion, p.
We besides learned some information about how the sample proportion is distributed:
Sampling Distribution of
For a random sample of size n such that n≤0.05N (in other words, the sample is less than five% of the population),
Why are these important? Well, suppose we have a sample of 100 online students, and find that 74 of them are part-fourth dimension. You might recall that based on information from elgin.edu, 68.5% of ECC students in full general are par-fourth dimension. So is observing 74% of our sample unusual? How do we know - we need the distribution of !
And then what we do is create a examination statistic based on our sample, and then use a tabular array or engineering to find the probability of what we observed. Hither are the details.
Testing Claims Regarding the Population Proportion Using P-Values
In this first section, we assume we are testing some claim well-nigh the population proportion. As usual, the post-obit 2 weather must be true:
- np(1-p)≥10, and
- north≤0.05N
Stride one : State the null and culling hypotheses.
| Two-Tailed H0: p = p0 Hi: p ≠ p0 | Left-Tailed H0: p = p0 H1: p < p0 | Right-Tailed H0: p = p0 H1: p > p0 |
Step two : Decide on a level of significance, α, depending on the seriousness of making a Blazon I fault. ( α volition frequently be given as part of a test or homework question, merely this will not be the instance in the exterior world.)
Stride 3 : Compute the test statistic, 
.
Step 4 : Decide the P-value.
Step v : Pass up the null hypothesis if the P-value is less than the level of significance, α.
Stride 6 : Land the conclusion.
Calculating P-Values
Right-Tailed Tests
Left-Tailed Tests
Two-Tailed Tests
In a two-tailed test, the P-value = 2P(Z > |zo|).
Information technology may seem odd to multiply the probability past 2, since "or more extreme" seems to imply the area in the tail only. The reason why we exercise multiply by two is that even though the effect was on i side, nosotros didn't know earlier collecting the data, on which side it would be.
The Force of the Evidence
Since the P-value represents the probability of observing our result or more extreme, the smaller the P-value, the more than unusual our observation was. Another style to look at it is this:
The smaller the P-value, the stronger the prove supporting the alternative hypothesis. We can use the following guideline:
- P-value < 0.01: very stiff evidence supporting the culling hypothesis
- 0.01 ≤ P-value < 0.05: strong evidence supporting the alternative hypothesis
- 0.05 ≤ P-value < 0.ane: some bear witness supporting the alternative hypothesis
- P-value ≥ 0.1: weak to no prove supporting the alternative hypothesis
These values are not difficult lines, of course, but they can requite u.s. a general thought of the strength of the evidence.
But wait! There is an important caveat here, which was mentioned before in the section near The Controversy Regarding Hypothesis Testing. The problem is that information technology's relatively easy to get a large p-value - just get a really large sample size! So the chart above is really with the caveat " assuming equal sample sizes in comparable studies, ..."
This isn't something every statistics text volition mention, nor will every instructor mention, but it's important.
Case one
According to the Elgin Community College website, approximately 56% of ECC students are female. Suppose we wonder if the same proportion is true for math courses. If we collect a sample of 200 ECC students enrolled in math courses and observe that 105 of them are female person, practice we take enough prove at the x% level of significance to say that the proportion of math students who are female person is different from the general population?
Annotation: Be sure to cheque that the conditions for performing the hypothesis examination are met.
[ reveal answer ]
Before we brainstorm, we need to make sure that our sample is less than five% of the population, and that np0(1-p0)≥x.
Since there are roughly 16,000 students at ECC (source: www.elgin.edu), our sample of 200 is clearly less than v% of the population. Also,
np0(1-p0) = 200(0.56)(1-0.56) = 49.28 > 10
Step one :
H0: p = 0.56
Hi: p ≠ 0.56
Step ii : α = 0.1
Footstep 3 : 
.
Step 4 : P-value = 2•P(Z < -i.00) ≈ 0.3187
(Note that this is a 2-tailed examination.)
Step 5 : Since P-value > α, nosotros do non turn down H0.
Footstep half dozen : There is not plenty evidence at the v% level of significance to support the claim that the proportion of students in math courses who are female is different from the general population.
Hypothesis Testing Regarding p Using StatCrunch
- Get to Stat > Proportions > One sample > with summary.
- Enter the number of successes and the number of observations.
- Enter p0 and H1, then press Calculate.
The results should be displayed.
Example 2
Consider the extract shown below (also used in Example ane, in Department 9.3) from a poll conducted by Pew Research:
Stem jail cell, marijuana proposals pb in Mich. poll
A recent poll shows voter support leading opposition for ballot proposals to loosen Michigan's restrictions on embryonic stem cell inquiry and permit medical use of marijuana. The Epic-MRA poll conducted for The Detroit News and television stations WXYZ, WILX, WOOD and WJRT found 50 per centum of likely Michigan voters back up the stem cell proposal, 32 per centum against and 18 percent undecided. The telephone poll of 602 likely Michigan voters was conducted Sept. 22 through Wed. It has a margin of sampling mistake of plus or minus four percentage points. (Source: Associated Press)
Suppose nosotros wonder if the percent of Elgin Customs College students who support stem prison cell enquiry is different from this. If 61 of 100 randomly selected ECC students support stalk cell inquiry, is there enough evidence at the v% level of signficance to support our claim?
Note: Be certain to check that the conditions for performing the hypothesis test are met.
[ reveal answer ]
Before we begin, we need to make sure that our sample is less than 5% of the population, and that np0(1-p0)≥10.
Since there are roughly 16,000 students at ECC (source: world wide web.elgin.edu), our sample of 100 is clearly less than five% of the population. Likewise,
np0(1-p0) = 100(0.50)(ane-0.l) = 25 > 10
Footstep one :
H0: p = 0.5
Hone: p ≠ 0.five
Pace 2 : α = 0.05
Step 3 : We'll apply StatCrunch.
Step four : Using StatCrunch:
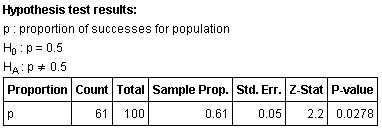
Step 5 : Since P-value < α, we reject H0.
Pace half-dozen : Based on this sample, there is enough evidence at the 5% level of significance to support the merits that the proportion of ECC students who back up stem cell research is different from the Michigan poll.
One question y'all might accept is, "What do we exercise if the conditions for the hypothesis examination about p aren't met?" Nifty question!
In that example, we can no longer say that sample proportion, , is approximately normally distributed. What we do instead is return to the binomial distribution, and just consider 10, the number of successes. Let'south practise a quick review of binomial probabilities.
A Binomial Refresher
The Binomial Probability Distribution Office
The probability of obtaining x successes in north independent trials of a binomial experiment, where the probability of success is p, is given by
Where x = 0, 1, two, ... , north
Using Technology to Summate Binomial Probabilities
Here'southward a quick overview of the formulas for finding binomial probabilities in StatCrunch.
Click on Stat > Calculators > Binomial
Enter northward, p, the appropriate equality/inequality, and x. The figure below shows P(10≥3) if n=four and p=0.25.
Hypothesis Testing Using the Binomial Distribution
Example 3
Traditionally, about lxx% of students in a particular Statistics form at ECC are successful. If only 15 students in a class of 28 randomly selected students are successful, is there enough evidence at the 5% level of significance to say that students of that particular instructor are successful at a charge per unit less than 70%?
[ reveal respond ]
If we consider the proportion of students who were successful, we can see that np(1-p) = 28(0.7)(1-0.7) = 5.88, which is less than 10. Therefore, the distribution of volition not be normally distributed.
Pace ane :
H0: p = 0.7
Hane: p < 0.7
Footstep 2 : α = 0.05
Step 3 : We'll apply StatCrunch.
Step 4 : If we let X = the number of students who were successful, X follows the binomial distribution. For this example, n=28 and p=0.70, and we desire P(X≤fifteen). Using StatCrunch:
Step 5 : Since P-value < α (though it's very shut), we refuse H0.
Footstep 6 : Based on this sample, there is enough testify at the v% level of significance to support the claim that the proportion of students who are successful in this professor's classes are less than 70%. (Keep in mind that this assumes the students were randomly assigned to that class, which is never the example in reality!)
Source: https://faculty.elgin.edu/dkernler/statistics/ch10/10-2.html
0 Response to "How To Find Binomial Probability On Statcrunch"
Post a Comment